ENFOQUE LAGRANGIANO DEL MOVIMIENTO DE LOS FLUIDOS

Para la descripción de un campo de flujo, se pueden adoptar dos enfoques:

•          Descripción Lagrangiana.- En honor del matemático francés J. L. De Lagrange, 1736-1813.
•          Descripción Euleriana.- En honor de matemático suizo L. Euler, 1707-1783.

Estos enfoques tienen que ver con el observador respecto al fenómeno cuyo movimiento se estudia.

Descripción Lagrangiana.

Se usa cuando el observador estudia una partícula siguiéndola a través de su movimiento en el flujo. Este enfoque es amplia mente usado en la mecánica de partículas y/o cuerpos indeformables, siendo que los principios básicos de la mecánica fueron establecidos con este enfoque

Se trata de identificar una pequeña masa de fluido en un flujo, denominada “partícula fluida”, y describir el movimiento todo el tiempo. 

Como la partícula está en movimiento su posición es una función del tiempo, y por consiguiente cada una de sus coordenadas es una función de posición:

x=x(t);             y=y(t);             z=z(t)

A lo largo del seguimiento de las partículas, (x, y, z) no son coordenadas fijas, sino que cambian con respeto al tiempo.

La trayectoria de una partícula de fluido está dada por el vector, y se expresa en coordenadas cartesianas como:

r(t) = x(t)i + y(t)j + z(t)k

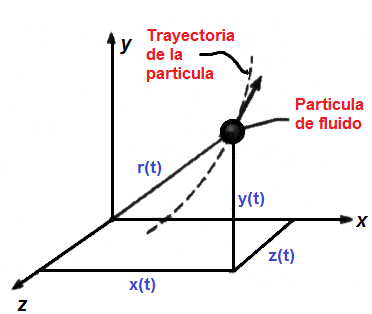Figura 1. Trayectoria y Velocidad de Una partícula de fluido

Una vez posicionada la partícula en el espacio en un instante dado se puede indicar su velocidad en ese punto en ese instante. La velocidad del fluido se obtiene al derivar la función posición con respeto al tiempo, y queda:

Donde:

 u, ν, y ω son las velocidades componentes en sus respectivas direcciones de coordenadas.

Las variables independientes son la identidad de la partícula y el tiempo. 
Esto representa solo una partícula. Para obtener una descripción más completa y general del movimiento del fluido en algún campo, se tendría que tener disponible las trayectorias de muchas partículas de fluido.

Una descripción Lagrangiana es atractiva si se trata de un número de partículas pequeño. Si todas las partículas se mueven como un sólido rígido o si todas las partículas se desplazan solamente un poco de su posición inicial o su posición de equilibrio. Sin embargo, en un fluido en movimiento, identificar y seguir el rastro de varias partículas es virtualmente imposible. Surgen complicaciones adicionales debido a que una partícula típica de fluido con frecuencia experimenta un desplazamiento largo. Por estas razones, en la mecánica de fluidos la descripción Lagrangiana no es muy útil.