Gráfica de un Pato en MatLab, usando métodos numéricos
En el siguiente ejercicio se pretende graficar el perfil de un pato usando métodos numéricos, en especial el tema de Interpolación polinomial fragmentaria o por partes (picewise). Este método crea una función cúbica entre cada punto y posteriormente lo evalúa es por ello que es posible visualizar la curva.
El ejercicio fue extraído del libro Análisis Numérico de Richard L. Burden y J. Douglas Faires, se desarrolló en Matlab y se grafico. Cabe resaltar que la siguiente metodología no se puede aplicar únicamente a figuras, sino, también a la vida real, como aproximaciones a curvas que no siguen una función específica, en hidráulica para el Diagrama de Moody, etc.
La Figura 1 muestra a un
joven pato en pleno vuelo. Para aproximar el perfil de la parte superior del
pato, seleccionamos algunos puntos a los largo de la curva por donde queremos
que pase la curva de aproximación. El Cuadro 1 incluye las
coordenadas de 21 puntos de datos relativos al sistema de coordenadas
sobrepuestas que aparecen en la Figura 2. Obsérvese que
se utilizan más puntos cuando la curva cambia rápidamente que cuando lo hace
con más lentitud.
Figura 1.
Representación de un Pato
El sistema de referencia relativo se realizo en el programa AutoCad, en la siguiente imagen se observan los puntos que se necesitaron para graficar el pato.
Figura 1.
El pato en un plano cartesiano
En los siguientes cuadros se muestran las coordenadas x, f(x) del pato (Figura 2), Estas
coordenadas sirvieron para la programación del pato en Matlab.
|
Núm.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
|
x
|
0.9
|
1.3
|
1.9
|
2.1
|
2.6
|
3
|
3.9
|
4.4
|
4.7
|
5
|
6
|
7
|
8
|
9.2
|
10.5
|
11.3
|
11.6
|
12
|
12.6
|
13
|
13.3
|
|
f(x)
|
1.3
|
1.5
|
1.85
|
2.1
|
2.6
|
2.7
|
2.4
|
2.15
|
2.05
|
2.1
|
2.25
|
2.3
|
2.25
|
1.95
|
1.4
|
0.9
|
0.7
|
0.6
|
0.5
|
0.4
|
0.25
|
Cuadro 2.
Coordenadas de la parte inferior A del pato
|
Núm.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
x
|
0.817
|
0.897
|
1.022
|
1.191
|
1.510
|
1.834
|
2.264
|
2.962
|
3.624
|
4.202
|
4.499
|
4.779
|
5.109
|
5.527
|
|
f(x)
|
1.180
|
1.065
|
1.023
|
1.010
|
1.032
|
1.085
|
1.192
|
1.115
|
1.087
|
1.100
|
0.830
|
0.608
|
0.350
|
0.106
|
Cuadro 3.
Coordenadas del ala superior del pato
|
Núm.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
x
|
4.659
|
4.865
|
5.085
|
5.261
|
5.387
|
5.478
|
5.527
|
|
f(x)
|
-5.161
|
-4.741
|
-3.933
|
-2.951
|
-1.970
|
-0.981
|
0.106
|
Cuadro 4.
Coordenadas del ala inferior del pato
|
Núm.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
x
|
4.659
|
4.750
|
4.990
|
5.289
|
5.560
|
5.839
|
6.113
|
6.606
|
6.916
|
7.305
|
7.563
|
7.802
|
7.983
|
|
f(x)
|
-5.161
|
-5.259
|
-5.284
|
-5.268
|
-5.161
|
-4.982
|
-4.769
|
-4.286
|
-3.911
|
-3.213
|
-2.670
|
-2.176
|
-1.655
|
|
Núm.
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
|
x
|
8.141
|
8.473
|
8.832
|
9.337
|
9.887
|
10.572
|
10.995
|
11.501
|
11.923
|
12.364
|
12.763
|
13.300
|
|
|
f(x)
|
-1.138
|
-0.434
|
-0.514
|
-0.494
|
-0.382
|
-0.005
|
-0.090
|
-0.085
|
-0.030
|
0.093
|
0.120
|
0.250
|
Cuadro 5.
Coordenadas del ojo superior del pato
|
Núm.
|
1
|
2
|
3
|
4
|
|
x
|
2.663
|
2.700
|
2.805
|
2.886
|
|
f(x)
|
2.202
|
2.279
|
2.293
|
2.222
|
Cuadro 6.
Coordenadas del ojo inferior del pato
|
Núm.
|
1
|
2
|
3
|
4
|
|
x
|
2.663
|
2.720
|
2.826
|
2.886
|
|
f(x)
|
2.202
|
2.130
|
2.143
|
2.222
|
Para obtener la gráfica del pato se realizó un algoritmo en Matlab, se realizó un
código general y luego se procedió únicamente a introducir los puntos de las
coordenadas que se muestran en los cuadros del 1 al 6.
El código general es:
% código para
dibujar un pato
clear %limpiamos las variables
% 1. INICIAMOS A PROGRAMAR LA PARTE SUPERIOR DEL
PATO
n=21; %Debe modificar este valor en base al número de datos (Núm. de datos -1)
% Creamos dos
matrices uno para x y otro para f(x), (Estos
datos se modifican dependiendo de que parte del pato se quiere graficar)
x= [0.817 0.9 1.3 1.9 2.1 2.6 3.0 3.9 4.4 4.7 5.0 6.0 7.0 8.0 9.2
10.5 11.3 11.6 12.0 12.6 13.0 13.3];
a= [1.18 1.3 1.5 1.85 2.1 2.6 2.7 2.4 2.15 2.05 2.1 2.25 2.3 2.25
1.95 1.4 0.9 0.7 0.6 0.5 0.4 0.25];
% A partir de aquí no es necesario
modificar
% Creamos la
matriz y calculamos h (i)
h=zeros(1,n);
for i=1:n
h(1,i)=x(1,i+1)-x(1,i);
end
% cálculo de Alpha
alpha=zeros(1,n);
for i=2:n
alpha(1,i)=(h(1,i).\3).*(a(1,i+1)-a(1,i))-(h(1,i-1).\3).*(a(1,i)-a(1,i-1));
end
%Creamos las matrices l, mu y z
l=zeros(1,n+1);
l(1,1)=1;
l(1,21)=1;
mu=zeros(1,n);
z=zeros(1,n+1);
z(1,21)=0;
for i=2:n
l(1,i)=2*(x(1,i+1)-x(1,i-1))-h(1,i-1).*mu(1,i-1);
mu(1,i)=l(1,i).\h(1,i);
z(1,i)= l(1,i).\(alpha(1,i)- (h(1,i-1).*z(1,i-1)));
end
%Creamos la matriz c, b y d
c=zeros(1,n+1);
b=zeros(1,n);
d=zeros(1,n);
for i=n:-1:1
c(1,i)=z(1,i)-(mu(1,i).*c(1,i+1));
b(1,i)=h(1,i).\(a(1,i+1)-a(1,i))-(h(1,i).*(c(1,i+1)+2*c(1,i)))/3;
d(1,i)=(3*h(1,i)).\(c(1,i+1)-c(1,i));
end
% Creamos la variable de las funciones
for i=1:n
xi=x(1,i):0.01:x(1,i+1);
curva=a(1,i)+b(1,i).*(xi-x(1,i))+c(1,i).*(xi-x(1,i)).^2+d(1,i).*(xi-x(1,i)).^3;
hold on
plot(xi, curva, 'LineWidth',
1.5)
end
grid
%en este punto se definió los Label de los ejes y el titulo
xlabel('x ','FontSize',14
)
ylabel('f(x) ','FontSize',14
)
title('Gráfica Pato','FontSize',16) .
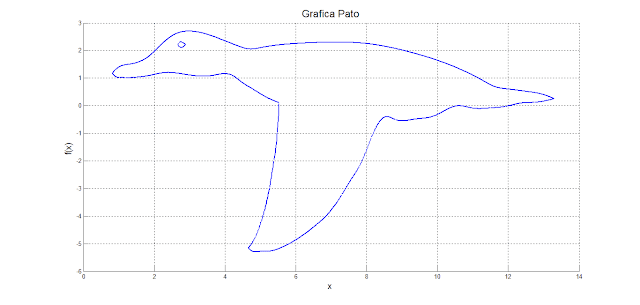
Ingresando las coordenadas que se muestran en los cuadros anteriores, y utilizando el algoritmo en MatLab es posible obtener la gráfica del pato, usando métodos numéricos.
Figura 1.
Gráfica de pato en Matlab
Este método ayuda cuando no conocemos información de la funcion que describe una curva y únicamente se tiene la curva.
En hidráulica sirve básicamente para:
-Determinar Coeficiente de Rugosidad del Diagrama de Moody.
-Coeficiente de descarga en vertederos.
-etc.
Bibliografía
- Análisis Numérico. Richard L. Burden y J. Douglas Faires. Grupo Editorial Iberoamericana S.A. de C.V.
- Apuntes de clases de la Materia Métodos Numéricos. Posgrado IMTA.






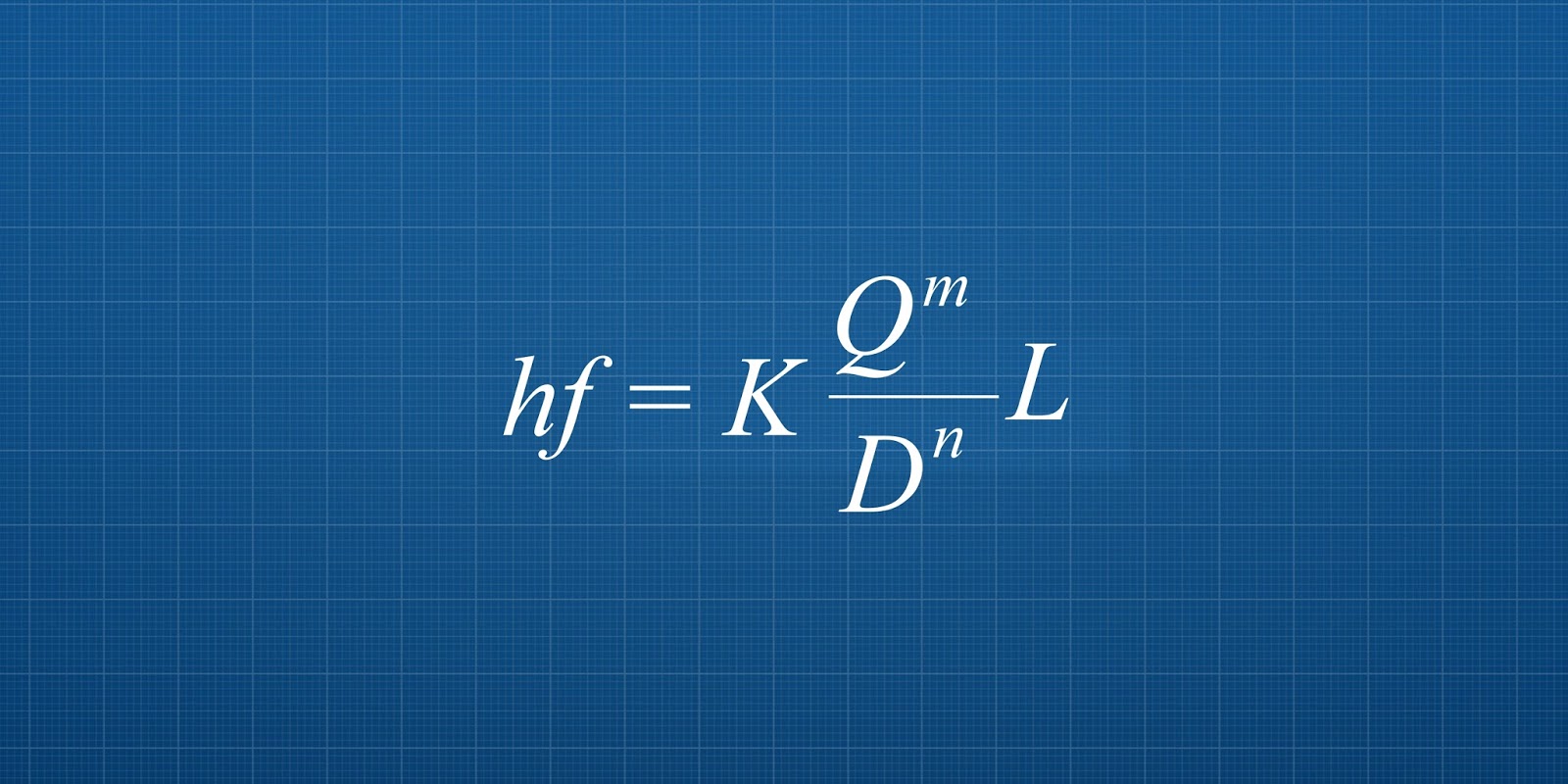

.png)


Comentarios
Publicar un comentario
déjanos tus comentario