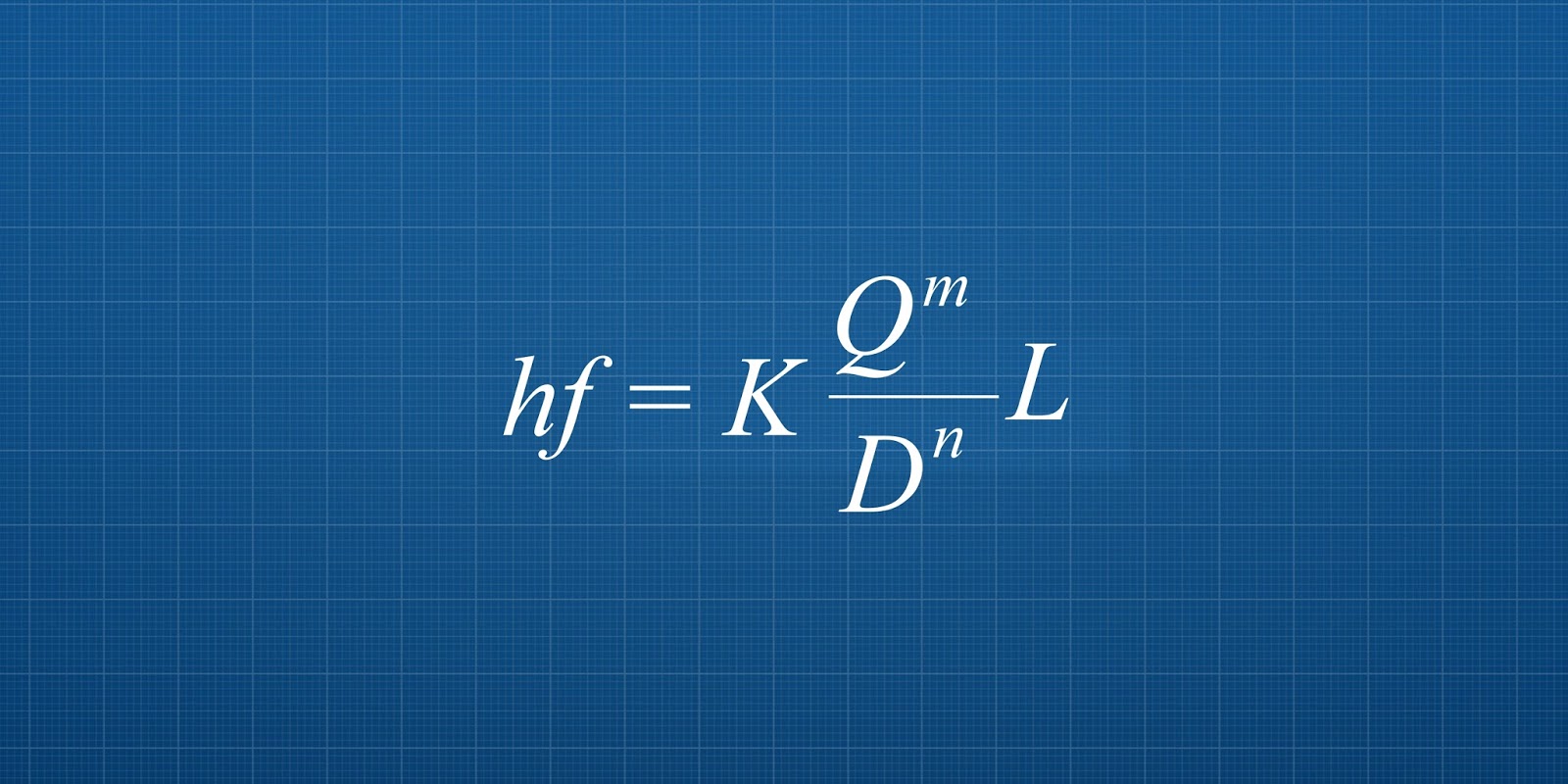Diseño hidráulico de tuberías con salidas múltiples mediante métodos numéricos
Introducción
En un sistemas de riego presurizado, comúnmente se encuentran dos tipos de tuberías: las ciegas y las de salidas múltiples (ya sea de servicio mixto o telescópicas), las ciegas se caracterizan por ser tuberías en donde el caudal que entra por un extremo es el mismo que sale al otro extremo, y se considera una tubería con salidas múltiples (TSM) cuando esta tiene salidas igualmente espaciadas y además en cada una de ellas se requiere extraer el mismo caudal (Martínez, 1991).
Para el diseño hidráulico de las TSM existen programas comerciales como WCADI, IRRICAD, IrrigaCAD, IrriMaker, etc, los cuales requieren licencias. Otra opción, sería el diseño manual que puede hacerse con Excel, el cual es tedioso y tardado, ya que por cada diámetro propuesto y por cada segmento (salida) se debe calcular la pérdida de carga por fricción.
En este sentido, en esta entrada se muestra como diseñar mediante métodos numéricos una tubería con salidas múltiples de servicio mixto (tramo de tubería en el que el diámetro y el tipo de material se mantienen invariables, que conduce y distribuye caudal), se utilizan los métodos por separado de newton Raphson y bisección tomando en cuenta la pérdida de carga permisible. En las TSM de servicio mixto comúnmente el diámetro es conocido por lo que el diseño se reduce a encontrar una longitud de la tuberia que permita que los emisores funciones con una cierta uniformidad. Estas TSM de servicio mixto suelen encontrarse con frecuenta en la línea regante de los sistemas de riego presurizados ya sea localizado o en aspersión, como por ejemplo las cintas de riego o microaspersores.
Para revisar como se diseñan las tuberías con salidas múltiples telescópicas (clic aquí), estas tuberías están constituidas por dos o más tramos de tubería con diámetro de diferente magnitud o tipo de material.
Materiales y métodos
A. Pérdida de carga por fricción
La pérdida de presión es la principal consideración en el diseño de cualquier tubería. La pérdida de carga de una tubería simple o ciega se determina con la expresión (1).
\[hf=K*\frac{Q^{m}}{D^{n}}*L\] | (1) |
Dónde: hf es la pérdida de carga por fricción; K involucra a un coeficiente de conversión de unidades y al coeficiente de fricción que depende de la fórmula empleada para cuantificar la pérdida de carga (Manning, Hazen-Williams, Scobey, Darcy-Weisbach, etc); Q es el caudal que circula en la tubería desde el inicio hasta el final de la misma; D es el diámetro interno de la tubería; L es la longitud de la tubería; m y n exponentes del caudal y del diámetro interno de la tubería, respectivamente.
Cuadro 1. Coeficientes y exponentes de las principales formulas empleadas para cuantificar la pérdida de carga por fricción
B. Pérdida de carga en tuberías con salidas múltiples
Este subtema se aborda a detalle en la entrada Pérdida de carga por fricción en "Tuberías con salidas múltiples". En resumen, en una tubería con salidas múltiples (TSM), a medida que el agua avanza, el caudal en el tubo se va reduciendo, por lo cual, la pérdida de carga por fricción en estas tuberías será de menor magnitud (Figura 1) que la pérdida de carga en una tubería simple sin salidas con las mismas condiciones (García & Briones, 2007).
Figura 1. Tubería con salidas múltiples. Primera salida al mismo espaciamiento que los emisores (Montiel, et al., 2002)
La pérdida de carga por fricción en una tubería con salidas múltiples (hfs) se puede determinar calculando la pérdida de carga en una tubería simple o ciega (hf) del mismo diámetro, longitud y con el mismo gasto de entrada, multiplicando sólo por un factor de salidas múltiples (F).
\[Hf_{s}=hf*F\] | (2) |
Para calcular el hf se usa la Ecuación 1 mientras que F se puede calcular usando la expresión de Christiansen (1942), Jensen & Fratini (1957) o Scaloppi (1988), según sea el caso de la condición de la distancia del inicio de la tuberia a la primera salida.
- Christiansen (1942)
\[F_{1}= \frac{1}{m+1}+\frac{1}{2N}+\frac{\sqrt{m+1}}{6N^{2}}\] | (3) |
Dónde; F1 es el factor de salidas múltiples de Christiansen; N es el número de salidas; m es el exponente del gasto en la fórmula usada para calcular la pérdida de presión causada por la fricción.
- Jensen & Fratini, (1957)
\[F_{2}=\frac{2N}{2N-1} \left [ \frac{1}{m+1}+\frac{\sqrt{m+1}}{6N^{2}} \right ]\] | (4) |
- Scaloppi (1988)
\[F_{3}=\frac{NF_{1}+ r_{s}-1}{N+r_{s}-1}\] | (5) |
Donde rs (S0/S) es la relación entre la distancia del inicio de la tubería a la primera salida (S0) y el espaciamiento constante entre salidas consecutivas (S).
C. Pérdida de carga permisible
La pérdida de carga permisible (hfp) indica la pérdida máxima de presion que se puede perder por fricción para que los emisores funciones con cierta uniformidad; esta hfp depende principalmente de pendiente del terreno, la presion de operación del emisor y de la máxima variación de presion entre el primer y ultimo emisor.
La hfp en la TSM, la cual dependiendo de su ubicación en el sistema (lateral o secundaria en aspersión o bien distribuidor en sistemas de goteo), es igual a un cierto porcentaje P (máxima variación de presion entre emisores) de la carga del emisor he, más la carga de presión que se gana por el desnivel a favor (dn) en la tubería (Montiel, et al., 2002).
\[hfp=P*he +d_{n}\] | (6) |
D. Diseño hidráulico
Para el diseño hidráulico de TSM de servicio mixto se empleó la Ecuación 2, y se sustituyó el valor de hfs por hfp; entonces de la Ecuación 1 y 2 resulta la Ecuación 7
\[hfp=K*\frac{Q^{m}}{D^{n}}*L*F\] | (7) |
\[Q=Qs*N\] | (8) |
\[L=S*N\] | (9) |
En caso de que exista una pendiente del terreno (%) se debe considerar en la hfp en términos de longitud L (Ecuación 9), es decir, la Ecuación 6 podría quedar de la siguiente forma:
\[hfp=P*he \pm \frac{Pendiente*L)}{100}\] | (10) |
\[hfp=P*he \pm \frac{Pendiente*(S*N))}{100}\] | (11) |
Sustituyendo las tres ecuaciones anteriores (8, 9 y 11) en la Ecuación 7 y usando las tres diferentes ecuaciones de factor de salidas múltiples y se iguala a cero, se tienen las siguiente funciones.
- Con F1 de Christiansen
\[f\left ( N \right )=\left [ K*\frac{(Qs*N)^{m}}{D^{n}} *(S*N)\right ]*\left [ \frac{1}{m+1}+\frac{1}{2N}+\frac{\sqrt{m+1}}{6N^{2}}\ \right ]- (P*he \pm \frac{Pendiente*(S*N))}{100})\] | (12) |
- Con F2 de Jensen & Fratini
\[f\left ( N \right )=\left [ K*\frac{(Qs*N)^{m}}{D^{n}} *(S*N)\right ]*\left [ \frac{2N}{2N-1} \left [ \frac{1}{m+1}+\frac{\sqrt{m+1}}{6N^{2}} \right ] \right ]- (P*he \pm \frac{Pendiente*(S*N))}{100})\] | (13) |
- Con F3 de Scaloppi
\[f\left ( N \right )=\left [ K*\frac{(Qs*N)^{m}}{D^{n}} *(S*N)\right ]*\left [ \frac{NF_{1}+ r_{s}-1}{N+r_{s}-1} \right ]-( P*he \pm \frac{Pendiente*(S*N))}{100} )\] | (14) |
Estas tres funciones tienen como característica común que la única variable desconocida es N, por lo que estas ecuaciones se deben resolver en función de N. Sin embargo, estas ecuaciones son no lineales, por lo que conviene resolverlo con métodos numéricos o en una hoja de calculo de Excel. En este caso por la practicidad se han seleccionado el método de bisección (Pseudocodigo 1) y el newton Raphson (Pseudocodigo 2).
Pseudocodigo 1. Bisección
Comentario: Para aplicar este método se ocupa de dos valores iniciales [A, B], los cuales son extremos, se realiza la evaluación en el punto medio de esos dos valores [en este caso es el número de salidas N], el punto medio va variar con respecto al número de iteración y si la función converge la diferencia entre el punto medio y los extremos se vuelve pequeña, por tanto, cuando se cumpla una cierta tolerancia se dice que hemos encontrado el valor que se buscaba. Comentario: El valor inicial A debe ser igual a cero, y el valor inicial B debe ser superior al número de salidas de la tubería con salidas múltiples, sin embargo, como esta longitud no se conoce este valor puede ser igual a 10,000.
Inician los cálculos Establecer el valor de los limites A=0,B=10,000 Calcular N=(a+b)/2
Repetir el ciclo -Se calcula el Caudal considerando N con la Ecuación 8 -Se calcula la longitud total L con la Ecuación 9 -Se sustituyen los valores en las Ecuaciones 12 - 14, según sea el caso. Con F1 de Christiansen se usa la Ecuación 12 Con F2 de Jensen & Fratini la Ecuación 13 Con F3 de Scaloppi la Ecuación 14 Tenido el valor sustituido en la ecuación seleccionada (Función de N) se hace una un análisis del resultados de f(N) Si f(N)>0 B=N; De lo contrario A=N; Termina el ciclo hasta que tolerancia |f(N)| <= 0.0000001 // se puede establecer otra tolerancia
Fin de los cálculos // Al encontrar el valor de N que satisface la igualdad se redondea y se sustituye en la Ecuación 9 para así obtener la longitud de la tubería. Esta longitud representa la longitud máxima que puede tener esa TSM para tener cierta uniformidad.
Pseudocodigo 2. Newton-Raphson
Comentarios Generales
-La ecuación general de newton Raphson es: xi+1=xi-(f(xi)/f'(xi))
-Adaptándolo en base al número de salidas, queda Ni+1=Ni-(f(Ni)/f'(Ni))
Dónde: Ni para la primera iteración es un valor inicial; f(Ni) es la función de pérdida de carga por fricción con salidas múltiples despejada (ecuación 12, 13 o 14); f’(Ni) es la derivada de la función.
Inician los cálculos
Comentarios- La derivada f’(Ni) se obtiene igual por métodos numéricos, usando el método de los cinco puntos. f'(Ni)=1/(12*h)*(-25*f(Ni0)+48*f(Ni1)-36*f(Ni2)+16*f(Ni3)-3*f(Ni4)). -h es un incremento con respecto al valor de la derivada, es este caso se seleccionó h=0.001. - Ni0=Ni; Ni1= Ni +h; Ni2= Ni +2h; Ni3= Ni +3h; Ni4= Ni +4h
Se establece el valor de Ni=1; //Es el valor inicial para la primera iteración
Repetir el ciclo
- Calcula f(N) de acuerdo a la Ecuación del 12-14 seleccionada, sustituyendo todos los valores y el valor de N
- Calcular f’(Ni) con el método de los cinco puntos
- Sustituir los valores de Ni , f(Ni0) y f’(Ni) en la Ni+1=Ni-(f(Ni)/f'(Ni)) y ahora el valor de Ni=Ni+1
- Calcular tolerancia; tolerancia= f(Ni0)/f’(Ni)
Hasta que |tolerancia|<= 0.0000001 // se cierra el ciclo si se cumple con la condición de tolerancia
Fin de los cálculos // Al encontrar el valor de N que satisface la igualdad se redondea y se sustituye en la Ecuación 9 para así obtener la longitud de la tubería. Esta longitud representa la longitud máxima que puede tener esa TSM para tener cierta uniformidad. Ejercicio
En esta sección se pone a prueba la metodología antes planteada, para ello se propone encontrar la longitud máxima permisible de la tubería de polietileno en base a los siguientes datos:
- caudal medio del emisor (Qs) es 37.5 l/h,
- diámetro interno (21 mm),
- espaciamiento entre emisores consecutivos es 2.5 m,
- espaciamiento entre el inicio de la lateral y la primera salida de 2.5 m (s), 1.2 m y 3 m.
Primero se calcula la pérdida de carga permisible con la ecuación 6. en este caso se trata de un terreno plano, sin embargo si tuviera una pendiente debe considerarse el desnivel.
Posteriormente, se calcula la longitud en base a los algoritmos anteriormente planteados, para ello se creó un script en Matlab y se obtuvieron los resultados mostrados en el cuadro 2.
Cuadro 2. Resultados de la longitud de las tuberías con salidas múltiples con distintos métodos y fórmulas.
De acuerdo al cuadro 2 se observa que con ambos métodos se llega al mismo resultado, el método de bisección es más sencillo de aplicar aunque se requieren más iteraciones que con el de Newton Raphson, sin embargo, actualmente esto no es un problema ya que cada iteración se lleva a cabo en milésimas de segundo con las nuevas computadoras.
Conclusiones
Se presenta un método para determinar la longitud máxima permisible de una tubería con salidas múltiples de un solo diámetro. Los dos métodos que se probaron brindaron resultados satisfactorios, esto indica que es posible diseñar estas tuberías con el uso de los métodos numéricos.
En el caso del método con newton Raphson, la derivada de la función complica el método, ya que no se puede obtener una derivada analítica de la función, sin embargo, se propuso el uso de otro método numérico para hallar dicha derivada. Este paso dificulto la aplicación del método, sin embargo, este método es muy útil ya que solo requiere un valor inicial y su convergencia es cuadrática.
En el caso del método por bisección, se requieren más iteraciones para llegar al resultado, sin embargo, es muy método muy sencillo de aplicar. Solo se debe tener cuidado al seleccionar el rango superior, este debe ser un valor muy grande (10,000) para que no sea menor al valor del número de salidas N que satisface la igualdad.
Referencias Bibliográficas
- Ángeles, V., 2016. Factores de ajuste para la pérdida de carga por fricción en tuberías con salidas múltiples telescópicas o con servicio mixto. Texcoco, Colegio Mexicano de Especialistas en irrigación, pp. 1-13.
- Ángeles, V., Arteaga, R., Vázquez, M., Carrillo, M., & Ibáñez, L. (2007). Factores de ajuste para la pérdida de carga por fricción en tuberías con salidas múltiples telescópicas o con servicio mixto. Ingeniería Del Agua, 14(4), 293–305. Obtenido de https://upcommons.upc.edu/bitstream/handle/2099/10589/III - V14N4.pdf
- Christiansen J., E. 1942. Irrigation by Sprinkling. California Agric. Experiment Station Bull. No. 670 University of California, Davis, Calif.
- Jensen M., C., and Fratini A., M. 1957. Adjusted “F” factors for sprinkler lateral design. Agric. Engrg., 38:4:247.
- Martínez, R., 1991. Riego localizado: Diseño y Evaluación. Texcoco, Estado de mexico: Universidad Autónoma Chapingo.
- Montiel, M., Angeles, J. & Herrera, J., 2002. Diseño hidráulico del sistema de riego parcelario. In: Manual para la elaboración y revisión de proyectos ejecutivos de sistemas de riego parcelario. México: s.n., pp. 5-1, 5-49.
- Scaloppi E., J. 1988. Ajusted “F” factor for multiple-outlet pipes. J. Irrig. And Drain Engrg, ASCE, 114:169-174.
